দুটি সদৃশ চতুর্ভুজের অনুরূপ কোণগুলো সমান এবং অনুরূপ বাহুগুলো সমানুপাতিক। দুটি চতুর্ভুজ সদৃশ হওয়ার শর্ত নির্ণয় করি।
| কাজ ১। তিন-চার জনের দল গঠন করে নিচের কাজগুলো কর: (ক) KLMN চতুর্ভুজটি আঁক, যার ∠ K = 45° KL = 3 সে.মি., LM = 2 সে.মি., MN = 3 সে.মি., NK = 2.5 সে.মি.। [ইঙ্গিত: প্রথমে ∠K কোণটি আঁক এবং কোণের বাহু দুটি থেকে KL ও KN সমান দূরত্বে দুটি বিন্দু চিহ্নিত কর। অতঃপর অপর দুই বাহু আঁক।। (খ) WXYZ চতুর্ভুজটি আঁক, যার WX = 6 সে.মি., XY = 4 সে.মি., YZ = 6 সে.মি., ZW = 5 সে.মি., ∠ w = 45°এ চতুর্ভুজটি কি অনন্য? (গ) KLMN ও WXYZ চতুর্ভুজের অনুরূপ বাহুগুলোর অনুপাত সমান কি? (ঘ) KLMN ও WXYZ চতুর্ভুজের অনুরূপ কোণগুলো পরিমাপ কর। সেগুলো কি পরস্পর সমান? (ঘ) KLMN ও WXYZ সদৃশ কি? |
লক্ষণীয় যে, দুটি সদৃশ চতুর্ভুজের
(ক) অনুরূপ কোণগুলো সমান এবং
(খ) অনুরূপ বাহুগুলো সমানুপাতিক।
দুটি চতুর্ভুজের অনুরূপ বাহুগুলো সমানুপাতিক হলে চতুর্ভুজ দুটি সদৃশ।
কাজ ১। নিচের চিত্রগুলোর সদৃশ জোড় চিহ্নিত কর। তোমার উত্তরের পক্ষে যুক্তি দাও।  |
উদাহরণ ১। ABC সমবাহু ত্রিভুজের AD, BE ও CF তিনটি মধ্যমা।
(ক) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ অঙ্কন কর।
(খ) দেখাও যে, ∠A = ∠B = ∠C
(গ) প্রমাণ কর যে, AD = BE = CF
(ক)
ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB = BC
(খ)
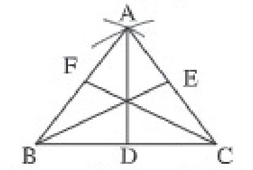
দেওয়া আছে, ABC সমবাহু ত্রিভুজের AB = AC = BC
প্রমাণ করতে হবে যে, ∠A = ∠B = ∠C
অঙ্কন: AD, BE ও CF তিনটি মধ্যমা অঙ্কন করি।
প্রমাণ: ABD ও ACD এ
AB = AC
BD = CD [∵ AD মধ্যমা]
AD সাধারণ বাহু
∵ ABD = ACD
∠ABD = ∠ACD
অর্থাৎ ∠B = ∠C
অনুরুপে দেখানো যায় যে
∠A = ∠B
∴ ∠A=∠B= ∠C
গ।
বিঃনি: দেওয়া আছে, ABC সমবাহু ত্রিভুজের AD, BE ও CF তিনটি মধ্যমা। প্রমাণ করতে হবে যে, AD=BE=CF
প্রমাণ: AB = AC. ∴ ABC সমবাহু ত্রিভুজ
AB = AC
BF = CE ∵ Fও E যথাক্রমে AB ও AC এর মধ্যবিন্দু।
BEC ও BFC এ
BE = CF
BC = BC সাধারণ বাহু
এবং অন্তর্ভুক্ত ∠BCE = অন্তর্ভুক্ত ∠CBF ∵ ∠B = ∠C
BEC = BFC
. BE = CF
অনুরুপে দেখানো যায় যে, AD=BE
AD = BE = CF
(প্রমাণিত)
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
